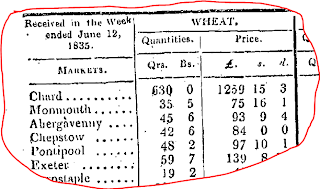Weather risk and the farmer

The 19th century farmer had much less control of the environment in which his crops were growing compared to modern farmers. But did weather risk get translated into different rents? After all, you'd expect a farmer who was wanting to rent land in an area where the weather was very changeable to try to negotiate a lower rent. It seems that the amount of rainfall in July matters a large amount for a grain crop such as wheat or barley. The coefficient of variation is a useful (and somewhat overlooked statistic). It is the standard deviation of a set of observations divided by their mean. So there are no units: it is just a percentage. Perfect for measuring "changeability" of weather. Malcolm kindly got me the CoV for July rainfall for 10 weather stations. I used GIS to interpolate between the stations, and then get the stretched values into the observations for our parishes. Then I ran a regression and --- wonderful news! --- CoV has a strong negative effect on rents. Greater CoV means lower rents. Below is a map of the southwest, showing the parishes and a raster of stretched CoV values. The highest CoVs are in the extreme southwest---that is Cornwall, well known for wet summers.

The pinkish bits have the lowest CoVs and it is no coincidence that wheat is grown there. The very wet areas are suitable for livestock and so that is where cattle and sheep raising went on.

Rent and distance from railway station

I am still working on the Railways Paper, trying to quantify the difference that an extra kilometre of railway track had on agricultural rents. The draft is very nearly finished, and I am hoping I can get the article into a journal such as Economic Geography.

So far I have found a significant relationship using two measures of the availability of railway track. One method is what I call the 'nearest station' method, which involves the measuring of the distance from the farm to the nearest railway station on an annual basis. As the railway was being built, it approached the farm. This meant that the farmer could put his animals into wagons for transport to market. He saved on the costs involved in droving the animals along roads (loss of weight, expenses and risk). So a reduction in distance to nearest station increased the rent...which is what we found. The other measure is the 'buffer' measure, which involves counting the total kilometres of railway track within a 40km radius of the farm. More track nearby raises the rent---it is easier to get your stuff to market. Greater "connectivity" in modern parlance.

Here are a couple of interesting graphs:

We have the rent rolls for 31 large estates. The graph shows the average rent and distance from nearest station. As theory predicts, rent is a declining function of distance. Now take a look at this one:

This is the distance between estate and nearest station over time. By 1860 or so, all the estates were within 10km of the nearest station. That accounts for the clustering around the 10 km mark in the first graph.

Surplus extraction!

Elasticity is a term used in economics to quantify the relationship between two variables in terms of percentages. Typically we use the price elasticity of demand. This means: “how many percent does demand change for a one per cent change in price?” If gas goes up ten per cent, how many per cent does demand change?

I am using elasticity to find how much agricultural rents changed for a change in price. This gives me an indication of how closely rents were oriented to market conditions. If landowners were setting their rents without really wanting to “squeeze” their tenants, then we would expect the elasticity to be small. Prices could change a lot, but the rent wouldn’t change very much. As the elasticity increases, this shows that landowners are beginning to set rents more competitively.

We can find elasticity using regression, if we first transform the variables to their natural logarithms. The coefficient is then the elasticity. I got a rent series for 1760 to 1840, and a price series, then did the transformation and the regression. Because I want to see the change in the coefficient over time, I used a technique called a ‘rolling’ regression. Here is the result:

You can see that the elasticity climbs up, reaching unity at about 1840. This is fascinating: landowners who were stuck with long leases during the time of big price increases during the Napoleonic Wars (ended 1815) got excluded from the windfall profits. So they renegotiated their leases to shorter ‘rack rent’ leases to scoop up the surplus. Greedy fellows, but we caught up with them!

The Ricardian method

The so-called Ricardian method has become quite popular in the last ten years as a way of trying to estimate the potential damage (or gains) to agriculture through climate change. It is usually a cross-sectional regression on land values (price of land per hectare or rent per hectare) and a bunch of exogenous variables. Records such as past wheat yields aren’t included. Then we can measure the impact of a change in a variable such as temperature or precipitation. Control variables, such as strength of the local economy are usually added.

I’ve been doing the same with the arable rents for the southwest of England in the early 19^th Century, but with recent meteorological data. There were no weather measurements taken then, and even if climate change has occurred in the period between 1835 and now, the change is likely to have been relative. The regression output is below, but here are some interesting points:

I include variables of interest, such as MARAIN (March rainfall) with their squares. That’s because there is a non-linear relationship. So for March rain, the regular unsquared variable has a negative sign, while the square is positive. The result of the combination on arable rents is a upward curve, meaning more rain was good in March. That is true: farmers want water in the ground to get the plant through to the summer.

But look at July rain. The signs are the opposite way round. The result is a curve, shown above. The recorded range of July rainfall in mm is on the x axis. The y axis is the rent. Some July rain is good, but then at about 52mm, that’s enough, thanks. The plant gets waterlogged and the forthcoming harvest is ruined.

Days of airfrost is fascinating: see the positive sign? Farmers wanted more days of airfrost back in 1835, because that is what killed the pests. No Roundup etc then. For soil, I put in dummies for different levels of clay. The negative signs mean that more clay lowers the rent. This seems counter-intuitive until one realises the connection with rainfall. Heavy clay soils tend to hold the water, generally good, unless you farm in a poorly drained area. Much of the southwest was just that. 

Agricultural production functions

Different types of agriculture have different manpower needs---at least they did in the early 19^th century. For a farm of any given size, less workers are required for livestock than for arable. Arable requires a lot of labour for sowing, weeding, harvesting, threshing and all the rest of it. So we might expect to see the number of workers per farmer increasing with an increasing share of arable. Now, here is the interesting thing. The ratio between arable and livestock changed with proximity to London, at least it did from the perspective of the southwest of England. The closer the farm was to London, the more arable. Cornwall, Devon , Dorset and Somerset were heavily into livestock.

So, how about we plot the ratio between arable and livestock against distance from London AND the ratio between number of labourers to farmers?  I have used lowess smoothing to get a single trend line from a mass of points. I have to say that I was really deeply surprised by the closeness of the two lines. And the best thing is that the data sources were entirely independent. The farmer to labourer ratio came from the 1851 Census records, and the arable to pasture ratio came from the 1836 Tithe Commission Files. The 'kink' at around 200km from London is the beginning of the heavily pastoral country, eastern part of Somerset. 

Von Thunen and intensification

JH von Thunen was a German farmer and economist who lived about 200 years ago (which makes him even older than me!). In the Devon rents paper, we successfully tested his theory that rents decline with distance from the market. He had another, less well-known theory. He argued that the intensity of agricultural production would increase the closer the farm was to the market. The rent would be higher, and so the farmer would 'work' his (or her!) land harder.

Amy and Malcolm,  you helped me to calculate the ratio between farmers and agricultural labourers, using data from the 1851 census. I built a shapefile using the locations and the ratios and then 'kriged' the shapefile to get an interpolated surface. I put the ratio values for each location into the observations for our 609 parishes in the southwest of England. Finally I plotted the ratio for each parish against its distance from London. The result is the graph below.

Isn't this fascinating? You can see quite plainly that the ratio decreases with increasing distance from London. The farmer employs less labour the further away he is from the market. The furthest distance represents Cornwall at the extreme west. There the ratio is very small, so probably most of the farmer's family were involved in work on the farm. Looks like von Thunen was right!

Direction for the railways paper

The focus of the ‘railways’ paper is a quantification of the amount of money saved by agriculture.  We are going to try to calculate the savings as a share of Gross National Product in the years 1850-1870.  Some previous studies (e.g. Hawke, 1970) conclude that the savings made by farmers using railways are “insignificant.”  Let’s test this!

Our methodology

1.      The graph shows the coefficient of the regression of rent against track length.  The coefficient provides the rent-per-acre increase for every extra kilometre of track within 40 km. of the estate.  The landlord is “extracting” this amount, equal to what the tenant farmer saves by using the railway.

2.      If we multiply the coefficient by number of acres by the length of track (year by year), this will give us the total amount saved. For example, take the year 1860. If a landowner had 1,000 acres, and in (say) 1860 200 km of track became available, then he would be able to gain an extra 1000*200*0.0002 = 40 pounds for that year and going on into the future. (I got the 0.0002 from reading off the graph).  But the point is that this saving is cumulative. We could (and we will!) go back to 1850, find the savings and then add that to the saving for 1851, and so on. The landowner gets the cumulative savings year after year. 

3.      At this point, we don’t care whether it was the landowner or the tenant who got the money.  It was saved, that’s enough.

4.      The result from paragraph 2 gives us the savings for our estates – now we need to extend this to the whole country.

5.      This isn’t too hard: Malcolm and I can calculate total track year by year, and Amy and I can find (where?!) total amount of pastoral land and cattle.

6.      The next step is to divide the total savings by the yearly GNP.

7.      Trying to get this done by the end of February!

1835 Wheat prices in colour!

I was looking for wheat prices in 1835 at a local level.  The 19^th century farmer sold his wheat production locally, so the local price was important.  We know the historical prices in London of course, but not throughout the country.  And it is the regional differences we want to find.

Here is how you -- Amy and Malcolm -- solved this data problem with me.  I approached wonderful Mary L. at UBC Library who is an authority on government data.  She found that wheat prices were published in the London Gazette at the market-town level.  That was enough!  A clip of a bit of the data source Mary found is here.

I selected 76 market-towns from the several hundred provided.  Malcolm got the geographical coordinates.  Amy put the old weights and money into shillings per quarter.  Using ArcGIS I built a “surface” with wheat price as the elevation.  The result is here.

You can see that wheat was cheaper in the Midlands and eastern counties, where it was grown.  Around the Southwest and London it was much more expensive.  Transport costs and demand drove up the price. This result isn’t really that much of a surprise – but how else could we have actually shown that what economic theory suggests actually takes place? And then, using ArcGIS I got the wheat prices at the highly localised parish level into the dataset...and guess what, it worked. So thanks Mary, Amy and Macolm.

Railway distance coefficients...a surprise!

The “Devon Rents” paper is pretty much done – the theory written up and the empirical section completed.  Now on to completing the Railways paper. 

Malcolm calculated kilometers of track and Amy worked on the rents for 25 estates over the period 1832-1870.  We found that an increase in track increased the rents – why?  Because the tenant farmer saved money by using the railways to take his cattle to market. However, he didn't get to keep the money. Those savings were “extracted” by the landowner as higher rent.  This is exactly what economic theory would predict.  So what’s new?

First, I plotted the coefficient of the length of track variable in the regression against time.  I found that the coefficient decreased over time. You can see this from the graph above. This means that for every extra kilometre of track, the landowner extracted a smaller amount year by year.  Why should this be?  Suddenly being soft-hearted?  I don’t think so! It’s more to do with competition among the railways.  They dropped their rates and so there was less to be extracted.  The graph shows it all.

Distance coefficients---positive?!!

Finally got it! I did two regressions:
Arable rent = arable yield + distance from London (and a bunch of other variables)
Pasture rent = pasture yield + distance from London

Agricultural location theory (and common sense) would tell us that the sign for yield should be positive (rent goes up for better land) and negative for distance from the main market. The further away you are, the more your transport costs, so your rent is less. So why was I getting negative signs for pasture (meaning livestock) and positive signs for arable? Seems contradictory. The pasture sign is fine---the animals had to walk all the way to London, so you would expect a negative. But arable?

I finally got it at about three this morning. Couldn't sleep. Wheat was produced in the eastern counties and the western counties were importers from the east. They could not produce enough to feed themselves. So those western producers who could grow wheat were in a sense protected by the distance. So the further you are away from London (which is close to the wheat-producing counties) the greater your arable rent.

I checked this by getting averages of wheat prices in 1820 for all counties (no data at the county level available for 1836). The map below shows that the west (darker colour for higher wheat prices) did have higher wheat prices. In effect Cornwall acted as a main market, which is why the prices are highest there. Here is the map.

London is the red dot to the east. The 588 parishes are coloured by their r-squared values. You can see there is patch of dark red (high r-squared) in north Devon/Somerset. Now I also made a graph of the regression coefficients for distance from London against distance from London. Here:

You can see that at the point closest to London (ie further from Cornwall) the regression coefficient is 0.00002. As we move towards Cornwall, the coefficient goes down to 0.000008, a reduction of 2.5 times. Notice the interest shape of the curve (which I think I can model). The 'straightest' or most linear section is between about 200,000 metres and 300,000 metres (marked with vertical red lines). It happens that our high r-squared values lie between these distances. The r-squared values are high because distance is being accurately incorporated.

It seems that the size of the coefficient is a function of distance. So if I can get the equation of the curve above, I can use integration to get the total cost of any journey....then plug that back into the regression. Hey the sun is finally shining!

Capitalisation in the southwest

Agriculture in the 1830s was very much in a state of change (does that make sense!), and one way of detecting rates of change on a regional basis is by calculating the ratio of farmers to the agricultural labourers employed. A higher ratio of employees to employer implies a greater degree of capitalisation. A smaller ratio means that much of the labour would have been supplied by the farmer and his family. Malcolm has found me the XY coordinates for 138 datapoints, and Amy and I have calculated the ratios. The datasource for the numbers of farmers and labourers is the 1851 census. Together we have created a 'surface' which interpolates between the 138 datapoint. The result is below. The surface is draped over an outline map of the southwest.

The darker the blue, the greater the ratio (goes from 0.97 to 14). There is an obvious pattern. The closer we go towards London, the higher the ratio. Similarly, the very low ratio in Cornwall seems to imply almost peasant subsistence. 

Update on the Devon rents paper

I haven't posted anything for about six months---so here is an update of the Devon rents paper. Here we have the data on 488 parishes in the southwest of England for the year 1836. We are trying to test the following five hypotheses:

H1: farmers were integrated into the national economy, even before the railways reduced transport costs
H2: agricultural rents were set  at levels predictable by agricultural location theory
H3: farmers considered weather risks when negotiating rent
H4: some landowners reduced rents in exchange for votes from their tenants
H5: the practice in the county of Devon of leasing agricultural land by auction increased rents in that county, other factors (such as land quality) being equal

I have finally managed to get a working regression, of arable rent against grain yield, elevation, distance to London and pasture rent for adjoining land. The coefficient of determination (r-squared) is a tad over 0.7, which is not at all bad (although of course I'd like it higher). I then used geographically-weighted regression to discover any regional differences in the regression coefficients. The result is below.

The colours represent different levels of r-squared, with red (in the green rectangle) being the highest. This means that for some reason the rents in the red parishes were set more closely in accordance with what agricultural location theory would predict. Why is this? Possible answers are:

1. There is a misspecification in the model, perhaps I've omitted a variable or two
2. John Knight bought 15,000 acres of Exmoor Forest in 1819, and that corresponds very closely to the green rectangle. Because he was a newcomer, the rents may have been set at more realistic levels
3. Agricultural leases in Devon were set by auction, in contrast to elsewhere. In this case we would expect the level of rent to reflect market conditions more closely than rents set arbitrarily.
4. More---I am working on this....but weather risk is an interesting possibility.

Just to keep you up to date. We are nearly there!